Comment améliorer les performances de vos campagnes Google Ads grâce aux analyses de régression ?

Les performances de vos campagnes SEA stagnent et vous aimeriez optimiser vos dépenses en la matière ? Avez-vous songé à utiliser pour cela des modèles mathématiques ? À l’ère du machine learning, les modèles statistiques de régression sont au cœur de la plupart des technologies d’analyse prédictive. Dans tous les secteurs d’activités, ils sont utilisés pour anticiper le comportement réel d’une cible numérique. Un promoteur immobilier qui veut estimer l’âge moyen d’un acheteur de villa de 120 m², un courtier spécialiste du rachat de crédits qui veut savoir quelle tranche de revenus contient le plus de consommateurs endettés, un assureur qui veut prédire le niveau de risque d’un contrat en fonction de variables liées au mode de vie des assurés : tous les trois ont en commun d’utiliser des modèles de régression pour effectuer leurs analyses.

  Dans le domaine du marketing digital et plus particulièrement des campagnes SEA, ces modèles sont également d’une grande utilité. Or, étant donné que peu de communicants savent réellement exploiter leur potentiel, ils permettent souvent de se distinguer par le haut des pratiques courantes et d’optimiser sensiblement la performance des publicités. Or, devinez quoi, les régressions statistiques ne sont pas réservées aux génies des maths ! Que diriez-vous d’apprendre à les utiliser pour optimiser vos dépenses Google Ads ?

Qu’est-ce qu’un modèle statistique de régression ?

Dans le domaine des statistiques, la régression est un ensemble de méthodes permettant de caractériser la relation entre une variable dépendante et une ou plusieurs variables indépendantes. Par exemple, si l’on veut établir un lien entre le revenu d’une personne (variable dépendante) et un certain nombre de variables indépendantes comme son âge, son sexe, son niveau de formation ou sa catégorie socio-professionnelle de référence, on peut utiliser un modèle de régression. Pour ce faire, on utilise soit une fonction linéaire (on parle alors de régression linéaire), soit un algorithme itératif (on parle alors de régression non linéaire). Dans les deux cas, la régression permet d’établir une fonction à partir d’un nuage de points. Voici un exemple de modèle de régression linéaire : 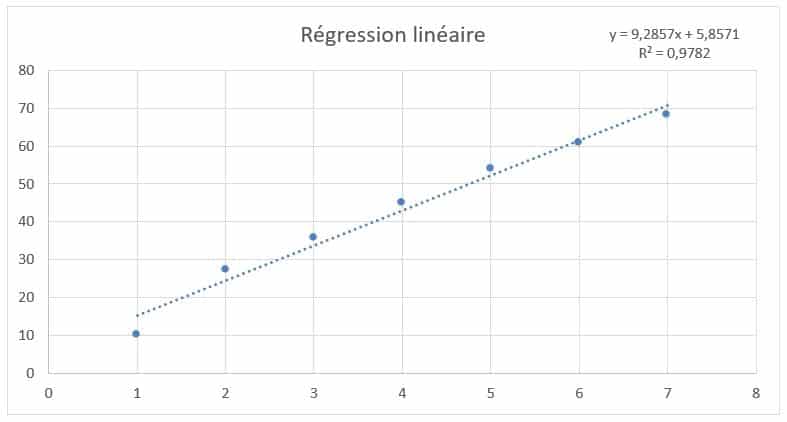    Et voici un exemple de modèle de régression non linéaire à partir des mêmes données :  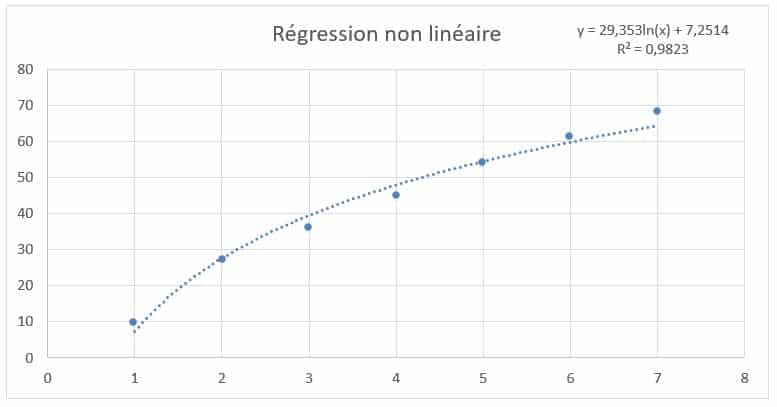   En l’occurrence, nous avons utilisé une fonction affine pour le modèle linéaire (f(x) = 9,2857x + 5,8571) et une fonction logarithmique pour le modèle non linéaire (f(x) = 29,353ln(x) + 7,2514). Ces deux fonctions modélisent la relation entre la variable indépendante x (dont les valeurs vont de 0 à 7) et la variable dépendante y (dont les valeurs vont de 10 à 68). Mais comment déterminer quel est le modèle qui décrit le mieux la relation entre x et y ? Nous utilisons pour cela le « coefficient de détermination », noté « R² », que nous avons fait figurer sur les graphiques ci-dessus. Pas de panique, Excel le calcule très bien à notre place ! Plus ce coefficient est proche de 1, plus le modèle est précis pour décrire la réalité. Dans notre exemple, c’est le coefficient de détermination du modèle non linéaire qui est le plus proche de 1. La fonction logarithmique devrait donc décrire la réalité avec plus de précision et permettre de meilleures prédictions que la fonction affine. Reste à savoir comment appliquer ces analyses de régression à des campagnes Google Ads…

Prédire le volume de conversions en fonction de la dépense publicitaire

L’utilisation la plus simple à mettre en pratique consiste à modéliser la relation entre les dépenses publicitaires liées à une campagne Google Ads et le volume de conversions résultant de cette campagne. Il s’agit donc ici d’établir une régression simple, puisque la relation concerne uniquement deux variables. Pourquoi ce choix ? Essentiellement pour deux raisons :

1. Il est bien sûr possible de réaliser des modèles de régression multiple (avec plus de deux variables), mais cela reste beaucoup plus compliqué à mettre en œuvre.
2. Toutes nos analyses tendent à montrer que la variable dont dépend le plus le volume de conversions est la dépense publicitaire, loin devant les autres variables.

Au regard de ces deux aspects, il y aurait peu d’intérêt à utiliser un modèle plus complexe, qui ne nous permettrait pas vraiment une analyse plus précise de la réalité. Restons-en donc à notre relation conversions / coût. Pour établir notre modèle de régression, nous avons extrait de Google Ads le rapport de campagne d’un de nos clients sur les trois premiers mois de l’année 2019. Nous avons besoin, pour chaque jour, du coût de la campagne (dépense engagée) et de la valeur des conversions (chiffre d’affaire généré). Cela nous donne un fichier Excel de cette forme : 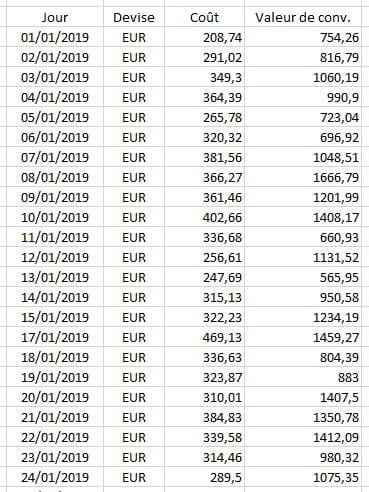    À partir des données des colonnes « Coût » et « Valeur de conv. », nous pouvons placer sur un graphique le nuage de points correspondant, avec le coût en abscisse et la valeur des conversions en ordonnée :  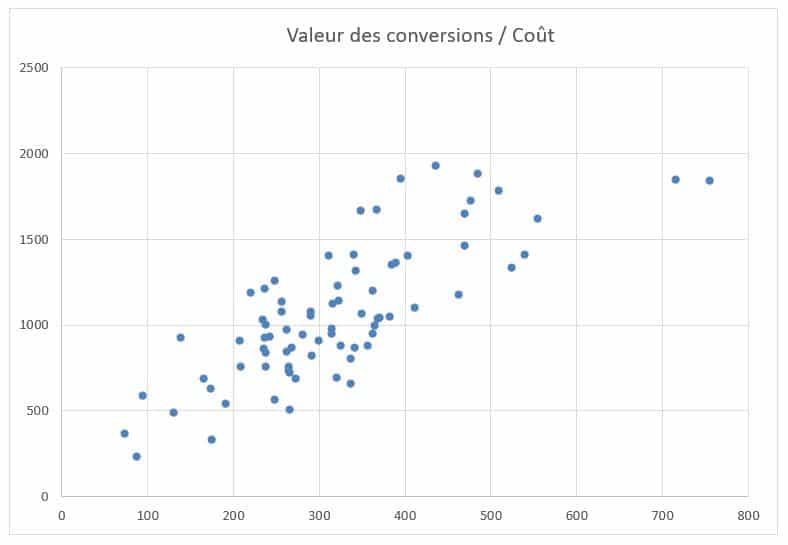   Il ne nous reste plus qu’à demander à Excel d’établir une régression en fonction de la répartition de ces points. Il suffit pour cela de faire un clic droit sur un point du nuage et de sélectionner « Ajouter une courbe de tendance ». En l’occurrence, nous opterons pour une fonction logarithmique. Une fonction polynomiale nous donnerait un coefficient de détermination plus proche de 1, mais elle ne serait pas adaptée à ce type d’analyses de régression (NDLR : nous reviendrons sur ce point dans la dernière partie de l’article).  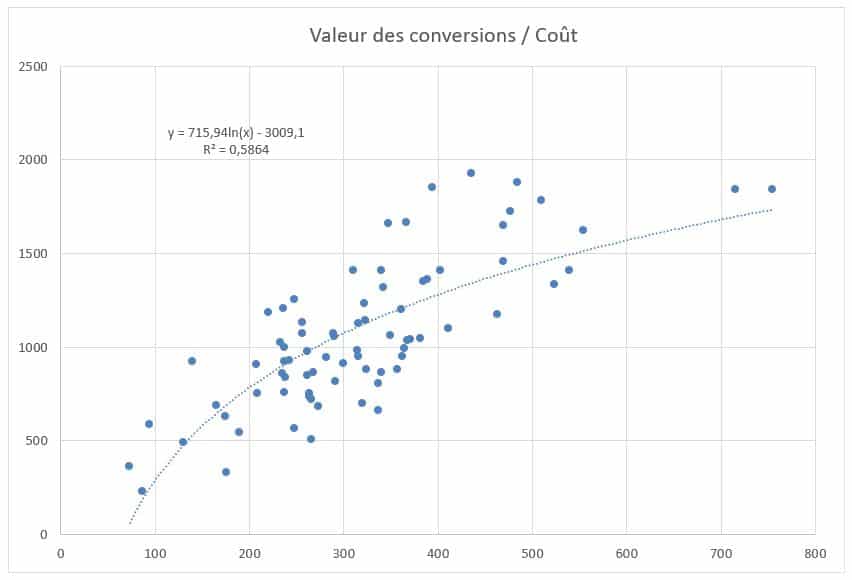   La fonction que nous avons obtenue, à savoir f(x) = 715,94 ln(x) – 3009,1, nous permet maintenant d’estimer le la valeur des conversions en fonction de n’importe quelle dépense publicitaire. Par exemple, si nous voulions connaître cette valeur pour une dépense de 2500 €, il nous suffirait d’effectuer le calcul suivant :  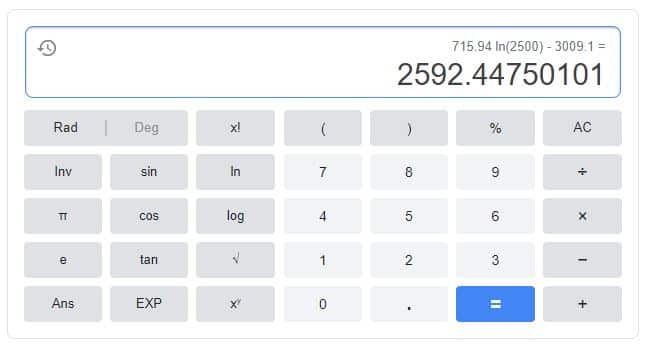   D’après notre modèle prédictif de régression, 2500 € de dépenses dans cette campagne Google Ads devraient donc entraîner 2592,45 € de conversions. Or l’exemple concerné dispose de peu de données dans les hautes dépenses. Il se peut donc que les faits ne vérifient pas exactement cette prédiction, notre modèle de régression étant plus fiable pour des dépenses inférieures à 2000 €, plus présentes dans nos données. Cela dit, ce modèle nous fournit une tendance faisant apparaître l’existence d’un plafond de conversions qu’il est difficile de franchir malgré une hausse des dépenses. Du reste, pour rester sur notre exemple, la régression statistique peut avoir une autre application aussi (voire plus !) intéressante : elle peut nous aider à trouver le meilleur compromis entre volume et rentabilité.

Optimiser la rentabilité d’une campagne

Le rapport Google Ads nous permet d’associer aux deux variables déjà étudiées d’autres variables comme le CPA (en l’occurrence le coût par conversion) et la marge dégagée. Partons ainsi d’un nouveau fichier Excel, qui intègre ces variables : 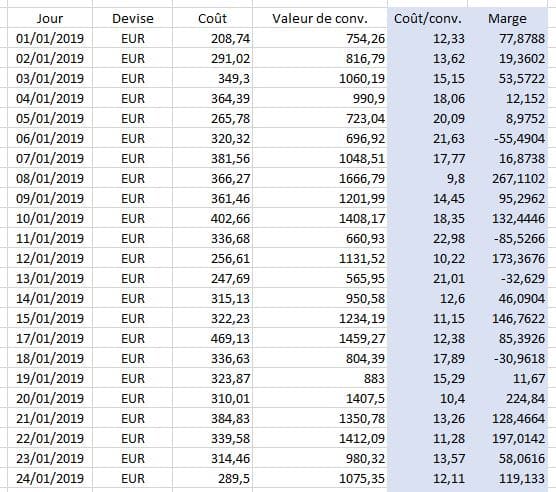    En cherchant cette fois à établir un modèle de régression entre les variables « Coût/conv. » (ou CPA) et « Marge », on obtient une fonction polynomiale plus intéressante à analyser :  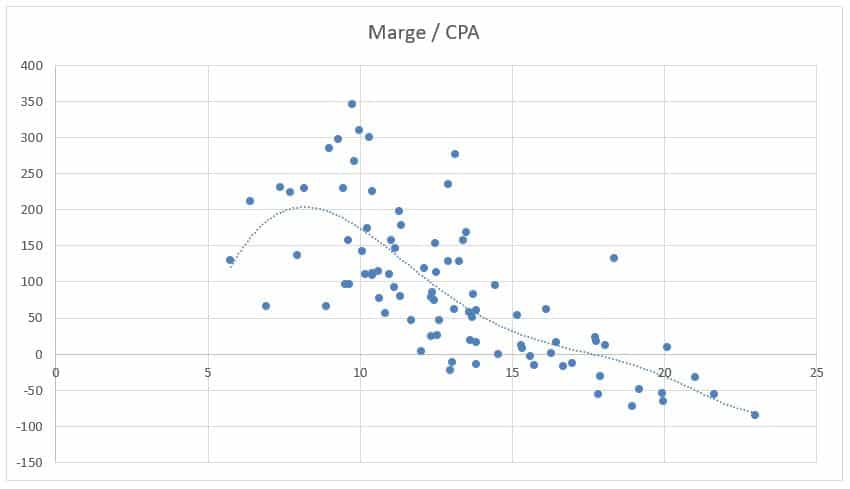   On constate ainsi qu’au-delà d’un CPA d’environ 8 €, la marge commence à décroître. Le sommet de la courbe représentant notre fonction nous permet alors d’établir que la meilleure rentabilité prévisionnelle de notre campagne correspond à un CPA compris entre 7 € et 9 €. Cela ne veut pas dire qu’il n’y a pas d’intérêt à pousser notre campagne au-delà de cette tranche de CPA (car on observe malgré tout que la marge reste positive jusqu’à un CPA d’environ 17,50 €), mais que notre campagne sera moins rentable au-delà de cette tranche. Si notre objectif d’optimisation prioritaire est la rentabilité, il vaut donc mieux ne pas dépasser un CPA de 10 €. Pour une analyse plus précise, on pourrait ensuite coupler ce modèle de régression à un modèle reliant par exemple la marge et le ROAS, afin d’affiner encore nos prédictions. Les couples de variables à analyser sont nombreux et certains sont susceptibles de nous fournir des modèles de prédiction pertinents. Il ne faut donc pas hésiter à les tester !

Limites des analyses de régression

Si les analyses de régression nous fournissent un puissant outil de prédiction, il faut toutefois les utiliser à bon escient et dans des conditions appropriées. Il est par exemple déconseillé de bâtir un modèle de régression à partir d’un volume de données trop faible. Cette méthode est donc à éviter sur de petits comptes ou sur des campagnes récentes. De même, il faut faire attention lorsqu’on utilise des données réparties sur une longue période. En matière de SEA, les marchés d’enchères évoluent parfois assez rapidement. Par conséquent, les données d’une campagne peuvent évoluer sensiblement sur une période de quelques mois. Aussi, nous recommandons généralement de ne pas utiliser des données datant de plus de six mois, au risque de fausser l’analyse de régression en y intégrant des caractéristiques de marché qui ne sont plus d’actualité. Il faut par ailleurs garder à l’esprit que l’on recherche avant tout à confirmer et chiffrer une tendance. Parfois, un algorithme qui semble décrire la réalité avec beaucoup de précision, parce qu’il a un R² proche de 1, peut vous induire en erreur dans votre analyse. Avant de faire appel aux modèles de régression, il faut donc avoir une idée du phénomène que l’on cherche. Par exemple, si l’on veut analyser le CA généré par rapport aux dépenses, on s’attend à obtenir une courbe amortie (le chiffre d’affaires ne pouvant pas croître à l’infini…). On utilisera donc une fonction logarithmique, comme dans notre premier exemple. En revanche, si l’on veut analyser la marge par rapport au CPA, on s’attend à obtenir une courbe en cloche. On utilisera donc plutôt une fonction polynomiale.

Conclusion

Pour faire un bon usage des analyses de régression, nous vous conseillons de garder à l’esprit les trois grands principes suivants :

1. Le rapport Dépense / Conversions est la première piste à exploiter avec les modèles de régression
2. S’il n’en ressort rien de très pertinent, il est tout de même intéressant d’optimiser ensuite vos campagnes en appliquant les modèles de régression à d’autres variables (marge, CPA, ROAS, etc.).
3. N’utilisez pas la régression si vous n’avez aucune idée de ce que vous cherchez. Si vous bâtissez mal votre modèle mathématique, vous en tirerez de mauvaises conclusions.

Vous voulez tester ces outils d’analyse sur vos campagnes ? N’hésitez pas à demander de l’aide à votre Account Manager.